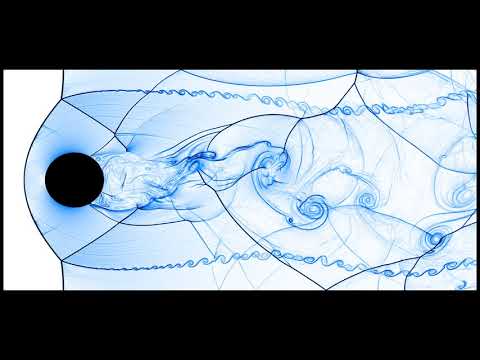
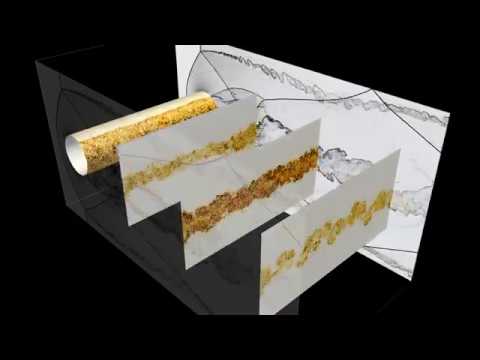
Ryujin is a high-performance high-order collocation-type finite-element solver for conservation equations such as the compressible Navier-Stokes and Euler equations of gas dynamics. The solver is based on the convex limiting technique to ensure invariant domain preservation and uses the finite element library deal.II (website) and the vector class SIMD library. As such the solver maintains important physical invariants and is guaranteed to be stable without the use of ad-hoc tuning parameters.
Ryujin is freely available under the terms of the Apache License 2.0 with LLVM Exception. Part of the contributed source code, third-party dependencies and header libraries are covered by different open source licenses. For details consult COPYING.md. Contributions to the ryujin source code are governed by the Developer Certificate of Origin version 1.1; see CONTRIBUTING.md for details.
Ryujin features the following equation modules selectable by the following parameter flags:
equation = euler, an optimized solver module for the compressible Euler equations with polytropic equation of state.equation = euler aeos, a generalized solver module for the compressible Euler equation with an arbitrary or tabulated equation of state.equation = navier stokes, an optimized solver module for the compressible Navier-Stokes equations with polytropic equation of state, Newtonian fluid model, and Fourier's law for the heat flux.equation = shallow water, a module for the shallow water equations.equation = scalar conservation, a module for scalar conservation equations with user-supplied flux. The module features a greedy wave-speed estimate to maintain an invariant domain, a generic indicator based on the entropy-viscosity commutator technique with a general, entropy-like function, and a customizable convex limiter.
A number of simulation results can be found on this youtube channel.
There original videos are available here (license details).
If you use this software for an academic publication please consider citing some of the following references:
@article{ryujin-2021-1,
author = {Matthias Maier and Martin Kronbichler},
title = {Efficient parallel 3D computation of the compressible Euler equations with an invariant-domain preserving second-order finite-element scheme},
doi = {10.1145/3470637},
url = {https://arxiv.org/abs/2007.00094},
journal = {ACM Transactions on Parallel Computing},
year = {2021},
volume = {8},
number = {3},
pages = {16:1-30}
}
@article{ryujin-2021-2,
author = {Jean-Luc Guermond and Matthias Maier and Bojan Popov and Ignacio Tomas},
title = {Second-order invariant domain preserving approximation of the compressible Navier--Stokes equations},
doi = {10.1016/j.cma.2020.113608},
url = {https://arxiv.org/abs/2009.06022},
journal = {Computer Methods in Applied Mechanics and Engineering},
year = {2021},
volume = {375},
number = {1},
pages = {113608}
}
@article{ryujin-2021-3,
author = {Jean-Luc~Guermond and Martin Kronbichler and Matthias Maier and Bojan Popov and Ignacio Tomas},
title = {On the implementation of a robust and efficient finite element-based parallel solver for the compressible Navier-stokes equations},
url = {https://arxiv.org/abs/2106.02159},
journal = {Computer Methods in Applied Mechanics and Engineering},
year = {2022},
volume = {389},
pages = {114250}
}
@article{ryujin-2023-4,
author = {Bennett Clayton and Jean-Luc Guermond and Matthias Maier and Bojan Popov and Tovar, Eric J.},
title = {Robust second-order approximation of the compressible Euler equations with an arbitrary equation of state},
url = {http://arxiv.org/abs/2207.12832},
journal = {Journal of Computational Physics},
pages = {111926},
year = {2023}
}
@article{ryujin-2024-5,
author = {Jean-Luc Guermond and Matthias Maier and Bojan Popov and Laura Saavedra and Ignacio Tomas},
title = {First-Order Greedy Invariant-Domain Preserving Approximation for Hyperbolic Problems: Scalar Conservation Laws, and p-System},
url = {https://arxiv.org/abs/2310.01713},
journal = {Journal of Scientific Computing},
year = {2024},
volume = {100},
number = {46},
pages = {},
}
@article{ryujin-2025-6,
author = {Jean-Luc Guermond and Matthias Maier and Tovar, Eric J.},
title = {A high-order explicit Runge-Kutta approximation technique for the shallow water equations},
url = {https://arxiv.org/abs/2403.17123},
journal = {Computers \& Fluids},
year = {2025},
volume = {288},
pages = {106493},
}
@article{ryujin-2025-7,
author = {Martin Kronbichler and Matthias Maier and Ignacio Tomas},
title = {Graph-based methods for hyperbolic systems of conservation laws using discontinuous space discretizations},
url = {https://arxiv.org/abs/2402.04514},
journal = {Communications in Computational Physics},
year = {2025},
volume = {38},
pages = {74--108}
}
@article{ryujin-2025-8,
author = {Jake Harmon and Martin Kronbichler and Matthias Maier and Eric Tovar},
title = {A conservative invariant-domain preserving projection technique for hyperbolic systems under adaptive mesh refinement},
url = {https://arxiv.org/abs/2507.18717},
year = {2025},
journal = {submitted}
}
For questions either open an issue, or contact Matthias Maier (maier@tamu.edu).
- Martin Kronbichler (@kronbichler), Ruhr University Bochum, Germany
- Matthias Maier (@tamiko), Texas A&M University, TX, USA
- Ignacio Tomas (@nachosaurus), Texas Tech University, TX, USA
- Eric Tovar (@ejtovar), Xcimer Energy Corporation, USA
- Wolfgang Bangerth @bangerth, Colorado State University
- Taylor Boylan (@tmboylan),
- Jerett Cherry (@jerret-cc), Colorado State University
- Gregory Christian (@gregorychristian, Imperial College London, UK
- Bennett Clayton (@bgclayto)
- Seth Gerberding (@Gerbeset), Texas A&M University, TX, USA
- Jake Harmon (@harmonj), Los Alamos National Laboratory, USA
- Jordan Hoffart (@jordanhoffart), Texas A&M University, TX, USA
- David Pecoraro (@ChrisPec27), Texas A&M University, TX, USA
- Madison Sheridan (@Helblindi), Texas A&M University, TX, USA