Wordnet

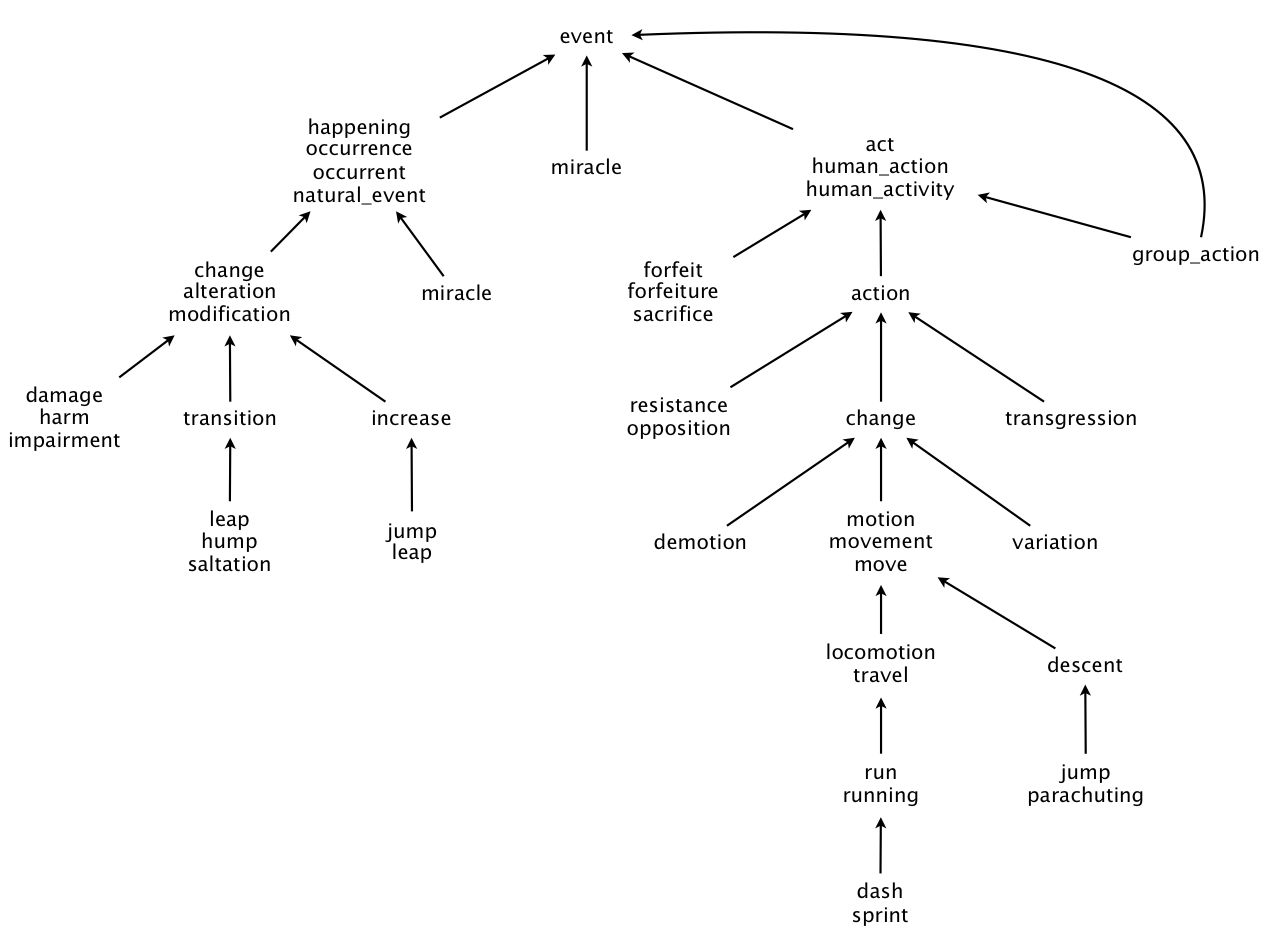
WordNet - это специальным образом сформированная база данных слов английского языка. WordNet используется в различных задачах компьютерной лингвистики и когнитивистики. Одним из примеров использования является компьютерная система Watson (IBM), разработанная для быстрого нахождения ответов в игре "Jeopardy!" ("Своя игра").

Как организована база WordNet:

Всё множество слов базы разделено на подмножества синонимов (synset). Множество синонимов - это множество слов, представляющих одно и то же понятие. Между некоторыми множествами синонимов может быть установлена семантическая связь одного из двух видов:

1. Понятие А является гипонимом (hyponym) понятия В, то есть понятие А выражает частный случай понятия В
2. Понятие А является гипернимом (hypernym) понятия В, то есть понятие В выражает частный случай понятия А

Зададим множество вершин V = {s | s -- это множество синонимов} и множество дуг E = {(a -> b) | a, b - множества синонимов; а является гипонимом b}. Тогда можно построить граф G = (V, E). G - ориентированный ациклический граф, имеющий одну корневую вершину.

Пример такого графа:

С помощью получившегося графа можно решать следующие две задачи.

Задачи

1. Определение семантической близости двух заданных слов A и B. Семантическая близость двух слов - это близость понятий, которые эти слова выражают. Задача усложняется тем, что одно и то же слово может выражать несколько понятий.

2. Выделение "лишнего" слова из заданного списка слов. "Лишнее" слово можно определить как слово, которое меньше всего семантически связано с остальными словами.

Решение задачи 1.

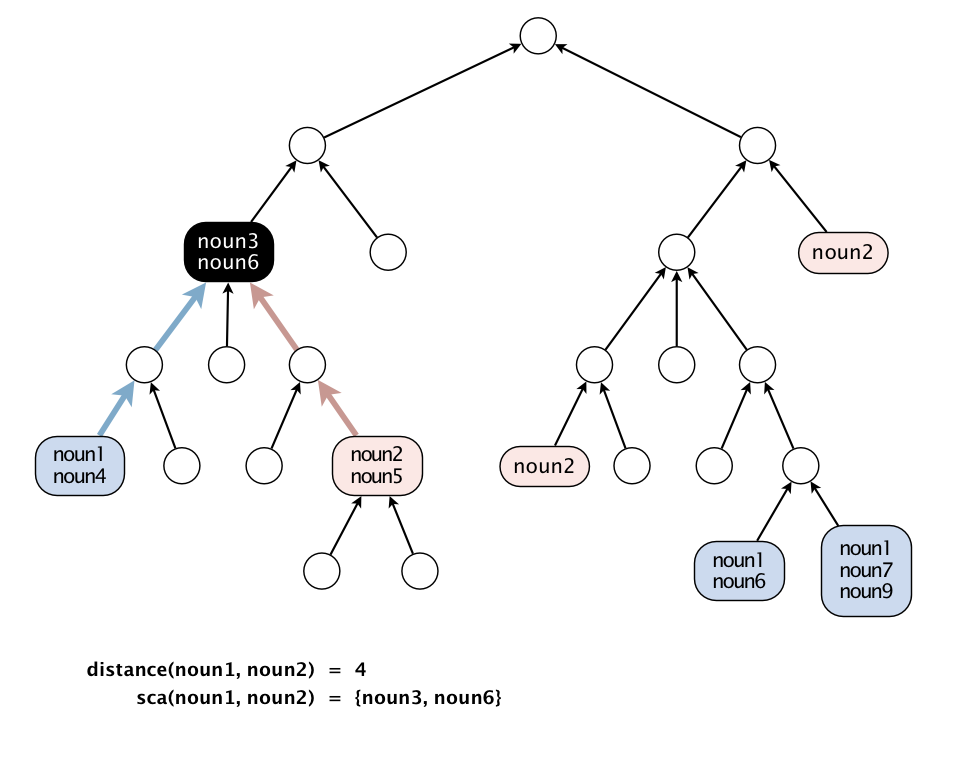
Для двух слов x и y определим

A = множество всех множеств синонимов(synset), содержащие слово x
B = множество всех множеств синонимов(synset), содержащие слово y

и вычислим

distance(x, y) = длина кратчайшего пути между множествами A и B
sca(x, y) = ближайший общий предок между A и B

Решение задачи 2.

Дано множество слов X = {x_i | i = 1..n}. Для каждого слова x_i определим его расстояние до множества остальных слов R_i = {x_k | k = 1..n, k != i}:

d_i = distance(x_i, x_1) + distance(x_i, x_2) + ... + distance(x_i, x_n)

Тогда решение задачи - это слово, имеющее наибольшее расстояние до множества остальных слов.

Реализация на C++

Для решения задач потребуется реализовать следующие классы:

1. Класс WordNet для хранения данных

class WordNet
{
public:
    WordNet(const std::istream & synsets, const std::istream & hypernyms);

    /**
     * Simple proxy class used to enumerate nouns.
     *
     * Usage example:
     *
     * WordNet wordnet{...};
     * ...
     * for (const std::string & noun : wordnet.nouns()) {
     *     // ...
     * }
     */
    class Nouns
    {
        class iterator
        {
            using iterator_category = std::forward_iterator_tag;
            // To do
        };

        iterator begin() const;
        iterator end() const;
    };

    // lists all nouns stored in WordNet
    Nouns nouns() const;

    // returns 'true' iff 'word' is stored in WordNet
    bool is_noun(const std::string & word) const;

    // returns gloss of "shortest common ancestor" of noun1 and noun2
    std::string sca(const std::string & noun1, std::string & noun2);

    // calculates distance between noun1 and noun2
    unsigned distance(const std::string & noun1, const std::string & noun2);
};

Входной поток synsets имеет формат CSV с тремя колонками:

• идентификатор множества синонимов (synset id)
• множество синонимов (synonyms)
• определение связанного понятия (gloss)

Входной поток hypernyms имеет формат CSV c переменным числом колонок:

• первая колонка - идентификатор множества синонимов
• оставшиеся колонки - список его гипернимов

Для эффективности реализации класса можно задать ограничение на длину строки слова и длину строки понятия.

Требования по эффективности класса WordNet:

• Конструктор класса должен иметь сложность не хуже O(N + M), где N и М - размеры входных файлов
• Метод bool is_noun(const std::string & word) const должен иметь сложность не хуже O(log N), где N - число слов
• Метод std::string sca(const std::string & noun1, std::string & noun2) const должен делать ровно один вызов ShortestCommonAncestor::lengthSubset()
• Метод unsigned distance(const std::string & noun1, const std::string & noun2) const должен делать ровно один вызов ShortestCommonAncestor::ancestorSubset()

2. Вспомогательный класс ShortestCommonAncestor для вычисления ближайшего общего предка

class ShortestCommonAncestor
{
   ShortestCommonAncestor(const Digraph & G);

   // calculates length of shortest common ancestor path from node with id 'v' to node with id 'w'
   unsigned length(unsigned v, unsigned w);

   // returns node id of shortest common ancestor of nodes v and w
   unsigned ancestor(unsigned v, unsigned w);

   // calculates length of shortest common ancestor path from node subset 'subset_a' to node subset 'subset_b'
   unsigned length_subset(const std::set<unsigned> & subset_a, const std::set<unsigned> & subset_b);

   // returns node id of shortest common ancestor of node subset 'subset_a' and node subset 'subset_b'
   unsigned ancestor_subset(const std::set<unsigned> & subset_a, const std::set<unsigned> & subset_b);
}

где Digraph - класс, описывающий граф G = (V, E).

Требования по эффективности класса ShortestCommonAncestor: конструктор и методы класса должны выполняться за время O(N_v + N_e), N_v - размер множества вершин V, N_e - размер множества дуг E.

3. Класс Outcast для вычисления "лишнего" слова из последовательности слов

class Outcast
{
public:
   explicit Outcast(WordNet & wordnet);

   // returns outcast word
   std::string outcast(const std::vector<std::string> & nouns);
};

4. Класс Digraph для описания графа понятий

class Digraph
{
...
};